Discrete Global Grid Systems

Contents

Discrete Global Grid Systems#

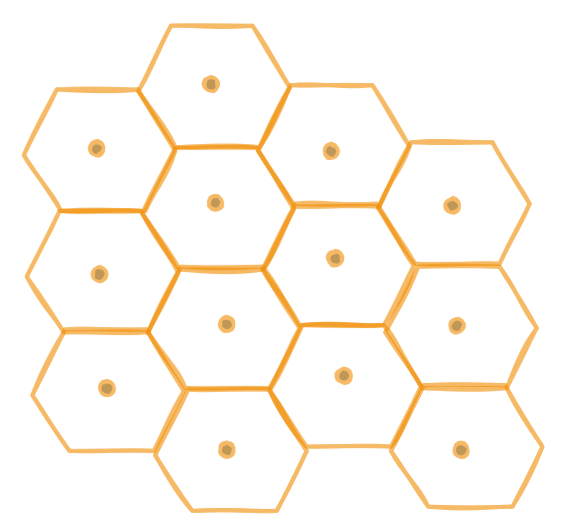
../_images/dggs.png

Fig. 3 The local grid structure of a hexagonal DGGS#

Projection-based grids have increasingly distorted grid cells the further away from the projection center / line they are.

Discrete global grid systems (DGGS) aim to minimize the distortion by approximating the surface of the earth (usually a sphere) by evenly subdividing it into planar faces. These faces are then recursively subdivided to form a hierarchy / tree of cells.

There is (in general) no way to arrange these cells into two dimensions that encode the topology, and thus in-memory we have to represent them as a 1D array (a list of cells).

healpix#

HEALPix (Hierarchical Equal-Area iso-Latitude Pixelization) has been developed for use in astronomy (cosmology). It divides the earth into 12 spherical rectangles (the “base pixels” or “base cells”), which are arranged in 3 rings with constant latitude. This means that there are four rectangles each that touch the poles, and there are another four that are centered around the equator. When going to a higher resolution, each side of the rectangle is subdivided by a constant factor \(n_{\mathrm{side}}\) (most commonly set to 2), resulting in \(n_{\mathrm{side}}^2\) new cells. All of these are also on rings of constant latitudes.

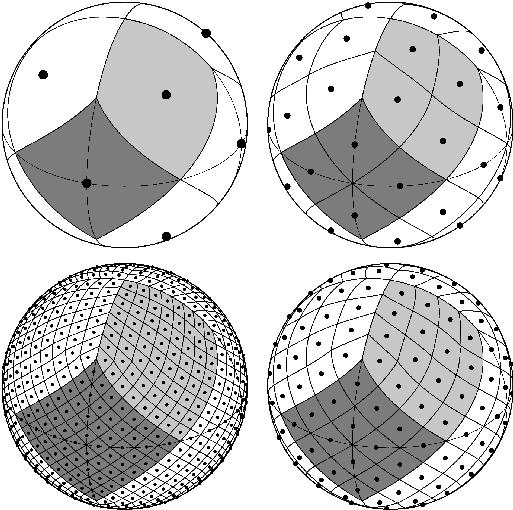
../_images/healpix.jpg

Fig. 4 The healpix grid (from https://healpix.sourceforge.io)#

There are three ways to number these cells:

  • the “ring” scheme, where the cells on a single ring of constant latitude have sequential numbers

  • the “nested” scheme, where each of the subdivisions follows a z-order curve

  • the “unique” scheme, which adds the resolution level (the number of subdivisions of the base cells) to the “nested” scheme using bitwise operations.

Contents